FAQ
CLASSIFICATION
>Attributes
TAXONOMY
FORMATION
Wall collapse
DIMENSIONS
Components
Terminology
>Synopsis
MEASUREMENT
Kolob Arch
Rainbow Bridge
Triangulation
Hopewell Arch
IDENTIFICATION
REFERENCES
Measuring the span of an arch with laser triangulation
by Jay H. Wilbur
There are, of course, many different ways to use triangulation to measure the span of a natural arch. This one assumes that you have clear line of sight to the key points on the arch, can range to these points very accurately, cannot directly measure angles with the same degree of accuracy, but can establish and measure the length of a baseline from which to range to the arch, and can ensure that this baseline is horizontal.
In this method we will establish and measure two triangles. These two triangles share a common base that is easily accessible and measured. The two vertices are the points of interest on the natural arch. We will measure the lengths of all sides of these two triangles using a laser ranger. Since the two triangles share a common base, that means we have to make 5 separate range measurements.
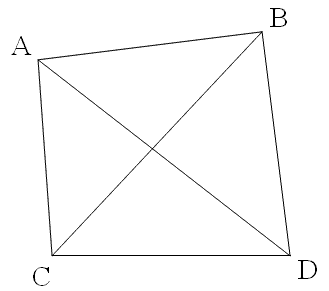
To explain how the method works, we start by examining the geometry we are trying to set up in two dimensions, i.e., a plane. Later we will examine how the reality of three dimensions affects the method. Beginning with the simplest case, plot four points on a piece of paper. Plot the four points so that they are approximately (but not exactly) the corners of a square. Label these four points A, B, C, and D, and draw connecting lines between all pairs of points.
The line AB is the dimension of the natural arch we wish to measure, i.e., the span. We establish the line CD as our baseline. The two triangles are ACD and BCD. We will range to measure the common base CD and the sides CA, CB, DA, and DB.
Measuring the lengths of all three sides of a triangle very accurately will enable us to calculate all of its angles with the same accuracy. Thus, after our ranging measurements, we will be able to accurately calculate angles DCA, DCB, CDB, and CDA. Subtraction then gives angles ACB and ADB with the same accuracy (as long as the four points are co-planar). Combining sides AC and CB with their included angle ACB lets us calculate side AB with the same accuracy. Similarly, combining sides BD and AD with their included angle ADB lets us calculate AB again. Measuring ranges only, we have determined the span to the same level of accuracy as our distance measurements. We did not have to measure any angles and we have two independent estimates of the same quantity.
Now comes the tricky part. What happens when you let in that third dimension? Well, first remember that three points determine a plane. Thus, points A, C, and D are always co-planar, as are points B, C, and D. This means we are never dealing with more than two planes that intersect along line CD, our baseline, which we are going to keep horizontal. Imagine point B floating straight up off the paper. Lines CB and DB lengthen and there is now an angle between the two triangles and the two planes they are in. Triangle ACD is still in the plane of the paper, but triangle BCD is at an angle to the paper. This means that angles ACB and BCD no longer sum to angle ACD, so our subtraction method doesn’t work accurately any more. A systematic error or bias has been introduced.
Using trigonometry and calculus, this bias can be estimated as a function of the amount of deviation there is from having four co-planar points. If the baseline is kept horizontal, then deviations from co-planarity are the result of selecting points A and B such that the line AB (i.e., the span) is not horizontal. In that case, and for small deviations, the bias in the method almost exactly offsets the bias in the span (from not being horizontal.) In other words, if the geometry is set up right for measuring the span this way, the biases roughly cancel. A 10-degree deviation from co-planarity (which would be easily detected by the human eye) only results in an error of half a percent when measuring the span.
Of course if this is not set up right, or larger deviations from co-planarity are present, this method doesn’t work. For example a 45-degree deviation would lead to an error of about 50%.
For more information on the subject of this article, see Measuring the Span of Hopewell Arch: A Simple Method Using Laser Ranges and Angles.