The Dimensions of Landscape Arch:

Removing the Uncertainty

by Jay H. Wilbur
June, 2004

Synopsis

Using laser technology and the NABS standard definitions for natural arch dimensions, a team led by the author re-measured Landscape Arch in June 2004, with a very high degree of accuracy and precision. Our results are that Landscape Arch has a span of 290.1 ± .8 feet, a height of 77.5 ± .5 feet, a width of 18.0 ± .5 feet, a thickness of 6 feet, and an opening breadth of 295 feet. These results indicate it is likely that, of the known contenders for the title of "largest" natural arch in the world, Kolob Arch has the greatest span. However, this can only be confirmed by measurements of Kolob Arch that equal the precision and accuracy of those now available for Landscape Arch.

[Update: Accurate measurements of Kolob Arch made after this paper was published indicate that Landscape Arch has a greater span than Kolob Arch. See The Dimensions of Kolob Arch. Also, arches in China have been identified with still larger spans. See our information on the world's giant arches.]

Introduction

Controversy has swirled around the dimensions of Landscape Arch, located in Arches National Park, for at least the past 20 years. In part, this controversy is driven by a desire to definitively determine the natural arch with the world's greatest span. For many, the natural arch with the greatest span should be given the title of the world's "largest" or "longest" natural arch. The span, a very precisely defined dimension, is preferred because terms like "largest" and "longest" are rather ambiguous when applied to natural arches and can't be quantitatively measured. Since its discovery, Landscape Arch has been a leading candidate for this title. The other contender is Kolob Arch in Zion National Park.

For many natural arches, the span is fairly easy to measure. For others, it can be very difficult. Unfortunately, for different reasons, both Landscape Arch and Kolob Arch fall into the difficult category. In the mid-1980s, two independent attempts were made to measure Landscape Arch. The results were inconsistent. At about the same time, two other independent attempts to measure Kolob Arch were made. Again, these results were inconsistent. Depending on whom you believed, a case could be made for either arch having the greater span. The published measurements were anything but clear-cut and certain. Questions were raised about the methodologies used on all four efforts. Hence, the controversy.

Until this year, there has been no further progress toward a definitive answer. Two recent developments, however, make new measurements desirable. The first of these is the ready availability of highly accurate laser ranging devices. The second is the publication of a standard, precise definition of the span of a natural arch. Although this definition is technical, its careful application ensures that span measurements are repeatable for a given arch and comparable for different arches. This eliminates many of the problems that plagued the earlier attempts. The definition, developed by the Natural Arch and Bridge Society (NABS), is available on their website, along with technical definitions for other natural arch dimensions.

In February 2004, Arches National Park granted the author permission to measure Landscape Arch. On June 7 and 8, 2004, he, along with sons Glen and Bryce and wife Judy, and with the assistance of park rangers Diane Allen, Sharon Brussell, and Murray Shoemaker, took new measurements of the arch using modern laser technology and the published dimension definitions. This effort was successful in obtaining very accurate measurements of Landscape Arch, including the span. Because these measurements are of standardized dimensions, they are both repeatable and comparable, e.g., to Kolob Arch should accurate, standardized measurements be obtained of that arch in the future. The cooperation and assistance of the Park in obtaining these results was essential and is gratefully acknowledged.

The following sections of this paper describe the methods used to measure Landscape Arch, summarize the measurements with analysis of their accuracy and precision, and discuss these results in the context of previous measurements and how they influence a determination of whether or not Landscape Arch has the greatest span of any natural arch in the world.

Methodology

Two obstacles must be overcome to measure Landscape Arch. The first of these is access. As a result of rockfalls in 1991 and 1995, the Park has closed the loop trail that once provided access to the area underneath the lintel. These rockfalls also obliterated most of the northern leg of the loop trail. In addition to safety concerns, the Park wishes to promote restoration of the fragile desert environment immediately under and around the arch. Thus, visitors are not allowed to access the arch beyond viewpoints on the main Devils Garden Trail.

Although we were granted special permission to access the area under the lintel, we were extremely anxious to minimize our disturbance of the grounds under restoration. We therefore limited our activities to two traverses directly under and in line with the lintel. Fortunately, most of this line lies along the old trail so disturbance was indeed slight. The first traverse, made on June 7, was used to reconnoiter the details of the arch's geometry, plan the span measurement, take height and width measurements at several points along the lintel, and place reference stakes. The second traverse, made on June 8, was used to obtain the span measurement and to remove the stakes and other signs of our activities. Photographs were taken from the main trail both for documentation and to obtain two other measurements, the thickness and opening breadth.

A second obstacle to taking measurements of Landscape Arch is the hill of soil-covered talus under the arch. By definition, the span is a horizontal dimension. The hill bulges up from a slanted line connecting the abutments of the arch and makes it difficult to keep a horizontal reference. Furthermore, there is an undulation in the hill that has a subtle synchronicity with the undersurface of the lintel. This makes it difficult to determine by inspection the point at which the height measurement should be taken.

The span measurement was kept horizontal by splitting it into three horizontal segments laid end-to-end, except that each segment was allowed to shift up or down along a vertical axis demarked by a laser plumb bob. Each segment was kept horizontal with a level built into the laser range finder, which was mounted on a tripod for stability. As it turned out, it was only necessary for one of the segments to be adjusted vertically by this method. The other two joined at a common point, the mount axis of the tripod.

To counteract the hill's undulations, height measurements were taken at several points along the lintel. The greatest of these then is the actual height of the arch.

Span and height measurements were taken using a Leica DISTO-classic laser range finder. Vertical reference was established using a LaserMark laser plumb bob. The Leica range finder has an advertised accuracy of a tenth of an inch over a range of 650 feet. Test ranging done prior to and during the measurements confirmed that the unit used was performing to this specification. The LaserMark plumb bob has an advertised accuracy of a tenth of a degree.

Although the lintel of Landscape Arch runs parallel with a field of sandstone fins that are aligned about 30 to 35 degrees off a true north axis, for simplicity's sake we refer to the arch and its parts with the four compass points, i.e., the north abutment, the east entrance, the west edge of the lintel, etc.

The south abutment of the arch presents an irregular profile. Figure 1 is a photograph of this profile taken looking east. Examination of the profile reveals a southward pointing indentation or notch in the abutment that extends the opening beyond where the abutment joins the base. The western edge of the back of this notch is the correct southern endpoint of the arch's span. This point is labeled "S" in Figure 2. Figure 2 depicts how the span was split into three segments to facilitate measurement.

Figure 1. A photograph looking east of the notch in the south abutment that extends the span southward from where the abutment joins the base.

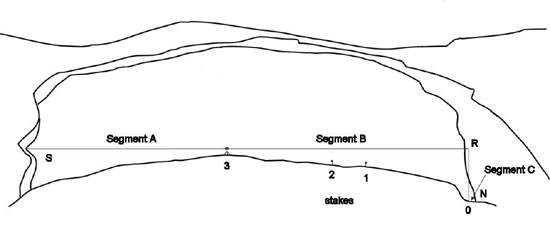
Figure 2. This figure is schematic and not drawn to scale. The span measurement was divided into three segments, A, B, and C. Segment A measures the horizontal distance from the correct point on the south abutment, point S, to a reference point, stake 3. Segment B measures the horizontal distance from stake 3 to a point R on the north abutment. Segment C measures the horizontal distance from stake 0, directly under R, to the correct point on the north abutment, point N. See text for the offset method used to find segment C. Stake 1 shows the approximate point where the width was measured. Stake 2 shows the approximate point where the height was determined.

The elevated notch in the southern abutment presents problems for other measurement methods but is advantageous for the laser ranging method used here. A point on the trail under the lintel was found such that the laser range finder could be placed on a tripod at the same elevation as S, i.e., the back of the notch. This point is labeled "stake 3" in Figure 2. Ranging in continuous mode from east to west across the back of the notch from stake 3 confirmed that the western edge was the correct point for the span measurement. Several direct ranges to point S were made to ensure an accurate measurement of the span segment A. Segment A (see Figure 2) is the horizontal, straight-line distance between point S, the western edge of the back of the notch, and stake 3.

Next, the laser range finder was swiveled on the tripod 180° in the horizontal plane and beamed to a point near the western edge of the north abutment. This point is labeled "R" in Figure 2. Several direct ranges to this point were made to ensure an accurate measurement of the span segment B (see Figure 2). The laser plumb bob was then used to find the point on the ground directly under point R. This point is labeled "stake 0" in Figure 2. Thus, segment B is the horizontal distance between stake 3 and R, and also between stake 3 and stake 0.

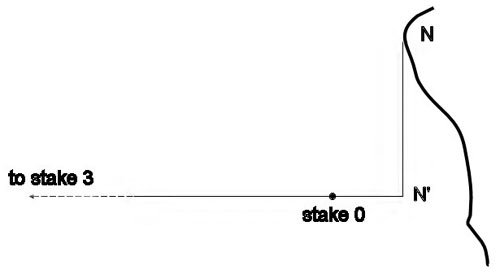
The correct northern endpoint of the arch's span is shown as point "N" in Figure 2. This point is not directly under the lintel, but is a few feet west of it. Figure 3 is a photograph documenting the location of this point. Because of this, as well as an interfering boulder, the final segment of the span, segment C, had to be measured as an offset.

Figure 3. The author uses a stick to point out the northern endpoint of the span. This is point N in figures 2 and 4.

To make this offset measurement, a target was placed at the vertex of a right angle. This vertex is labeled N' in Figure 4. One leg of the right angle connects points N and N'. The other leg is in the vertical plane defined by points R, stake 0, and stake 3. Thus, point N', as well as point S, are in this plane. The correct placement of the target at N' was accomplished using a sighting protractor with one leg pointing at N and the other pointing at both stake 0 and stake 3.

Figure 4. The offset viewed from above (the top of this figure is to the west, and the bottom is to the east). A target is placed at N' to measure segment C. Not drawn to scale.

The target was set at point N' and the laser range finder was used to directly measure the horizontal distance between stake 0 and N', i.e., segment C. Addition of the measurements for the three segments, A, B, and C, then is the first estimate of the span. Error analysis (see Results below) was then used to refine this estimate.

Height measurements were taken at several points along the underside of the lintel. At each selected point the laser range finder was used in continuous mode to find the vertical distance from the ground to the lintel. The largest of such height measurements was found at the point marked "stake 2" in Figure 2. This measurement is reported below as the height of the arch.

Since the sun was very near the zenith, measuring the width of the lintel's shadow was used as a very close approximation of the actual width. A single measurement was taken using a steel tape at the point where a minimum value was determined by inspection. Care was taken to keep the tape horizontal. The width measurement was taken at the point marked "stake 1" in Figure 2.

The thickness and opening breadth were determined by photographic analysis. An image of the arch was taken with a calibrated lens with a 35mm focal length from a point on the main trail that is at a measured distance from the arch. This image was used to measure the ratios of the thickness to the height and the opening breadth to the span. These ratios were then used to estimate the thickness and opening breadth. The thickness and opening breadth were also estimated using the geometry of the photograph, i.e., known distance to the arch and the focal length of the lens. The results were compared for a final estimate of these two dimensions.

Results

The span of Landscape Arch was determined by adding the measured span segments A, B, and C (see Figure 2), and then refining this estimate using error analysis. Segment A was measured as 113 feet, 5 inches. Segment B was measured as 170 feet, 11 inches. Segment C was measured as 5 feet, 7 inches. Thus, our first estimate of the span is 289 feet, 11 inches. However, this result needs to be refined as a result of both random error and some systematic biases.

First we look at the random errors involved in this estimate. The precision of the laser range measurements, less than an inch in all cases, is a negligible factor in the error budget. Because segments A and B share a common endpoint at the swivel point of the tripod mount, and because the laser was setup to measure from this point, any translation error resulting from this join is also less than an inch and is not a factor in the error budget. The error associated with shifting segment C vertically is a little larger. The vertical height between stake 0 and R was measured as 45 feet. The precision of the LaserMark plumb bob is 0.1 degree. Over 45 feet, this translates to a random error of about 1 inch. However, to account for any slight misplacement of the bob and stake, we estimate the random error here to be about 3 inches.

By far the largest random error was associated with placing the offset target at N'. We estimate it by assuming a 2-degree error in determining the right angle and sighting it along the line connecting N and N', a distance of 14 feet. This leads to an error estimate of about 6 inches. The root-mean-square of 6 inches and 3 inches yields the total expected random error of about 7 inches.

Some biases must be considered in refining the span measurement. It is unlikely that segments A, B, and C were exactly aligned with each other or with the horizontal. At the two junctures, slight deviations almost certainly occurred. These deviations from exact linearity bias the result, making it larger than a true result. However, we can estimate this bias and subtract it from our measurement to get a better estimate of the true span.

An upper bound on the deviation from the horizontal or from linearity is 3 degrees. This would translate into a range bias of about 2 inches at each of the two joins between the three segments. Thus, a worst-case bias would be 4 inches. To account for this, we reduce our estimated span value by half that amount, and increase the error bars by the other half. This puts the span at 289 feet, 9 inches, plus or minus 9 inches.

Another bias results from measuring S to N' instead of S to N. Computing the hypotenuse of the right triangle S-N'-N adds 4 inches to our result. Thus, the final, best estimate of the span is 290 feet, 1 inch, plus or minus 9 inches. Alternatively, this is 290.1 ± .8 feet. 290.1 feet is 88.4 meters.

As stated earlier, several height measurements were taken along the lintel. Since each of these was a direct range using the laser range finder, the precision of each is a fraction of an inch. The largest value obtained was 77 feet, 2 inches. The values obtained on either side of this value were about 75 feet. Nevertheless, because not every single point along the lintel was ranged, even our largest value must be considered a lower bound on the true height. Since it is unlikely that the true value would be more than a foot greater than the largest value obtained, we estimate the true height of the arch as 77.5 ±.5 feet. 77.5 feet is 23.6 meters.

As discussed above, the width measurement was obtained using a steel tape. The error associated with this measurement is estimated to be less than 3 inches. However, to be conservative, we report a width of 18.0 ± .5 feet.

Using photographic analysis, we report a thickness of 6 feet. This extraordinary result must be considered an upper bound. The thickness is probably a few inches less than 6 feet, but photographic analysis does not permit a more precise estimate. Our photographic analysis also led to an estimate for the opening breadth of 295 feet.

Discussion

In 1986, Robert Vreeland measured the span of Landscape Arch using a tape, gravity plumb bob, level, and other hand-assembled tools. His result was published in the January 2000 issue of SPAN (Vol. 12, No. 1). He reported a span of 290.4 ± .15 feet. An examination of Vreeland's methodology leads this author to the conclusion that Vreeland's reported error bars (± .15 feet) are overly optimistic. Given the complexity and number of segments measured, along with the dependency on several right angles and calculations, a more reasonable estimate of his error bars is 3 feet. It does appear that he made a reasonable effort to ensure a horizontal measurement and also selected the correct points to measure on both the north and south abutments. However, given the complexity of his method, it was certainly possible that an undetected bias or mistake might have crept into his result. Nevertheless, the close agreement between his result and the span reported here strongly supports a conclusion that he performed the measurement correctly and with as much accuracy as his method and equipment permitted.

In 1984, Dale Stevens measured several dimensions of Landscape Arch using a tape, transit, level, and other hand-assembled tools. His results were copied in the November 1990 issue of SPAN (Vol. 3, No. 1). He reported a height of 87 feet, a width (labeled "horizontal thickness" in the paper) of 15.5 feet, a thickness of 16 feet, and an opening breadth (labeled "light at widest place") of 306 feet, along with a number of other non-standard dimensions. He did not report a span measurement. Unfortunately, much confusion has resulted from some readers incorrectly assuming that his "horizontal line width," calculated to be 301 feet, was an estimate of the span. However, that dimension, the horizontal projection of the opening breadth, does not correspond with the standard definition for the span in the case of Landscape Arch. Stevens did not include any discussion of the accuracy or precision of his measurements.

It is interesting to compare Stevens' results for width, thickness, height, and opening breadth to those obtained in this investigation. His measurements were taken before the 1991 rockfall. This rockfall unquestionably decreased the width of the arch by several feet. It is, therefore, hard to explain why his width is significantly less than that found here. A pre-rockfall width of 15.5 feet must be viewed as incorrect. Using the current width of 18 feet and photographs, we estimate a pre-rockfall width of about 26 feet.

Another surprise is Stevens' reported thickness, 16 feet, which is significantly greater than the 6 feet reported here. Although photographic analysis is certainly less precise than some other methods, it cannot be that far off. Could the Stevens' number be a typographic error, i.e., 6 feet with a leading "1" incorrectly attached? In any case, it is very obvious from even a cursory examination of the lintel that the thickness is significantly less than the width. Stevens' results would indicate that they are about the same. This is an obvious error.

Stevens' reported height of 87 feet is also greater than the height reported here. In his paper, he indicated obtaining height measurements that varied from 79 to 92 feet. This suggests that Stevens may have been measuring total height, i.e., from the ground to the top of the lintel, rather than the standard height. In any case, although the 77.5 feet reported here might not be the absolute maximum height of the arch, it cannot be off by more than about a foot.

Finally, the opening breadth of 295 feet reported here is less than Stevens' 306 feet. Again, while photographic analysis of this dimension is not precise, it is doubtful that our estimate is off by 11 feet. It is not difficult to conclude that Stevens' results overall must be viewed as suspect.

Our last point of discussion is to examine how the current measurements affect a comparison of Landscape Arch with Kolob Arch for the title of "largest" or "longest" natural arch in the world. We now have a very accurate measurement of the span of Landscape Arch. Unfortunately, we do not have a reliable measurement of the span of Kolob Arch. Nevertheless, certain conclusions can be drawn from the measurements that have been reported.

[2006 update: Accurate measurements of Kolob Arch made after this paper were published indicate that Landscape Arch has a greater span than Kolob Arch. See The Dimensions of Kolob Arch.]

Reed Blake reported a span for Kolob Arch of 310 feet based on triangulation from a distance. These measurements were done in 1983. It is not clear from his report that his team measured the correct points of the span in accordance with the standard definition. Nor is it likely that they obtained the one-foot accuracy Blake claims. In 1984, Stevens measured Kolob Arch using photographic analysis. Stevens did not measure the span of the arch, but rather measured the opening breadth, which he called "widest light opening." However, in the case of Kolob Arch, the span and opening breadth should be fairly close. He obtained a value of 292 feet and did not report an expected error. The author also measured Kolob Arch using photographic analysis in 1992. The rather imprecise result of 294 ± 12 feet was obtained. However, in this case it is at least certain that the correct definition of the span was used and that the correct points were measured. The author believes it is impossible to get a more accurate measurement using photographic analysis, and that therefore Stevens' result should be viewed with a similar expected error.

Until more accurate measurements of Kolob Arch are obtained, it cannot be determined with certainty which arch has the greater span. Nevertheless, the author believes that the new, accurate measurement of Landscape Arch reported here, i.e., a span that is less than 291 feet, coupled with three independent results for Kolob Arch that are larger than 291 feet, make it probable that Kolob Arch has the greater span.

[2006 update: Accurate measurements of Kolob Arch made after this paper were published indicate that Landscape Arch has a greater span than Kolob Arch. See The Dimensions of Kolob Arch.]